最近要做一个旅游路线规划的应用，路线规划就是一个经典的旅行商问题

旅行商问题

旅行商问题（Travelling salesman problem, TSP）是这样一个问题：给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。
解旅行商问题有很多种算法，这些算法分两种：精确算法和近似算法，精确算法有：回溯法、动态规划等，近似算法有：贪心算法、蚁群算法、模拟退火算法、遗传算法等。
精确算法一定可以解出最优解，但是时间复杂度很高，近似算法的效率就比准确算法高得多，缺点就是有一定概率得不到最优解。但是在大部分情况下，他都能算出最优解，即便得不到最优解，算出来的近似解也是十分接近最优解的，故我决定采用近似算法。
上网查阅一些资料后我决定采用模拟退火算法。
模拟退火算法(Simulated Annealing，SA)最早的思想是由N. Metropolis 等人于1953年提出。1983 年,S. Kirkpatrick 等成功地将退火思想引入到组合优化领域。它是基于Monte-Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法，理论上算法具有概率的全局优化性能,目前已在工程中得到了广泛应用，诸如VLSI、生产调度、控制工程、机器学习、神经网络、信号处理等领域。

模拟退火算法

1. 退火
   在热力学上，退火（annealing）现象指物体逐渐降温的物理现象，温度愈低，物体的能量状态会低；够低后，液体开始冷凝与结晶，在结晶状态时，系统的能量状态最低。大自然在缓慢降温（亦即，退火）时，可“找到”最低能量状态：结晶。但是，如果过程过急过快，快速降温（亦称「淬炼」，quenching）时，会导致不是最低能态的非晶形。
   如下图所示，首先（左图）物体处于非晶体状态。我们将固体加温至充分高（中图），再让其徐徐冷却，也就退火（右图）。加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小（此时物体以晶体形态呈现）。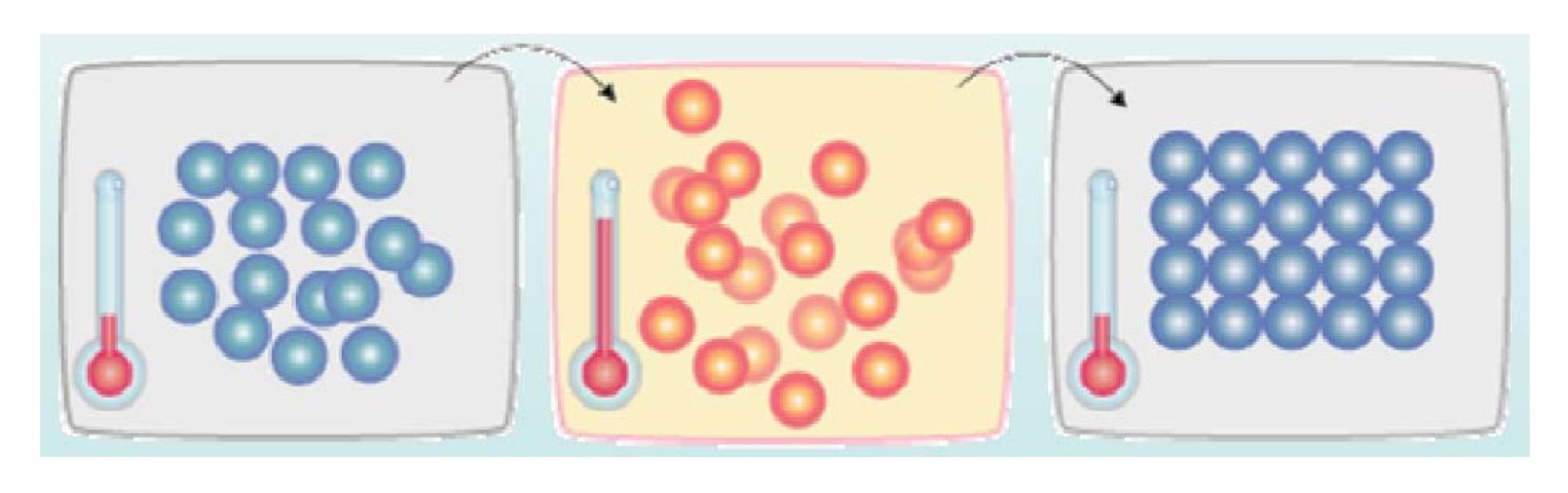
   
2. 模拟退火
   在下图这个函数中，我们想要去找到最优解C，如果我们采用贪心算法，我们从A点开始搜索，每一次搜索都取当前局面的最优解，那么当到达B点时，我们就会停止搜索。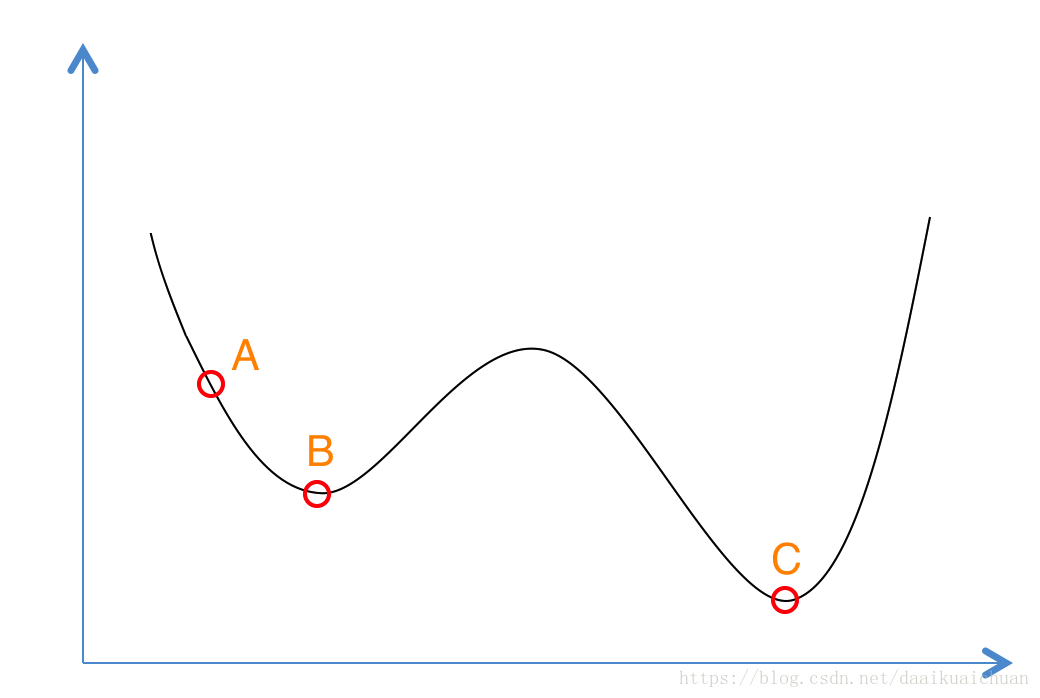
   
   模拟退火其实也是一种贪心算法，他也是在不断地搜索当前局面的最优解，但是它的搜索过程引入了随机因素。模拟退火算法会以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。
   当我们搜索到B点时，会有一定的概率去接受B点右边的不是局部最优的点，所以就有概率跳出局部最优解B，得到全局最优解C。
   总结：
   （1） 若f(x+1) <= f(x)，即新解优于当前最优解，则接受这个新解为当前最优解。
   （2） 若f(x+1) > f(x)，即新解不如当前最优解，则有一定概率接受这个新解为当前最优解。
   模拟退火算法从某一较高的温度出发，开始搜索当前最优解，一开始温度较高，变化的概率比较大，伴随温度参数的不断下降，变化的概率也逐渐下降，最后会逐渐趋向于稳定。
3. 代码

/** 初始温度 */
double T = 5000.0;

/** 温度下限 */
double T_min = 1e-8;

/** 退货系数 */
double r = 0.98;

/** 每个温度的迭代次数 */
int L = 100;

/** 总迭代次数 */
int countL = 0;

/** 退火次数 */
int countR = 0;

while(T > T_min){
  for (int i = 0;i < L ;i++) {

    /** 随机交换cop中两个点的顺序 */
    cop = randomCity(cop);

    /** 计算 result 和 cop 两条回路的长度  */
    double d1 = getDistance(result);
    double d2 = getDistance(cop);
    double de = d2 - d1;

    if (de <= 0){
        result = cop;
    }else {
        if (Math.exp(-de/T)>Math.random()){
            result= cop;
        }
    }

    countL++;
  }
  T = T * r;
  countR++;
}

System.out.println("最优解："+result);
System.out.println("退火次数："+countR);
System.out.println("总迭代次数："+countL);